Defining Jobs using Firetasks¶

This tutorial shows you how to:

Run multiple tasks within a single Firework
Run tasks that are defined within a Python function, rather than a shell script

This tutorial can be completed from the command line, but some knowledge of Python is helpful. In this tutorial, we will run examples on the central server for simplicity. One could just as easily run them on a FireWorker if you’ve set one up.

Introduction to Firetasks¶

In the Introductory tutorial, we ran a simple script that performed echo "howdy, your job launched successfully!" >> howdy.txt". Looking inside fw_test.yaml, recall that the command was defined within a task labeled ScriptTask:

spec:
  _tasks:
  - _fw_name: ScriptTask
    script: echo "howdy, your job launched successfully!" >> howdy.txt

The ScriptTask is one type of Firetask, which is a predefined job template written in Python. The ScriptTask in particular refers Python code inside FireWorks that runs an arbitrary shell script that you give it. You can use the ScriptTask to run almost any job (without worrying that it’s all done within a Python layer). However, you might want to set up jobs that are more powerful than shell scripts using Python programming. Later in this section, we’ll demonstrate how to accomplish this with custom Firetasks. However, first we’ll demonstrate the simplest version to linearly run multiple tasks.

Running multiple Firetasks¶

You can run multiple tasks within the same Firework (it might be helpful to review the Workflow Model diagram). For example, the first step of your Firework might write an input file that the second step reads and processes. Finally, a third step might move the entire output directory somewhere else on your filesystem (or a remote server).

Let’s create a Firework that:

Writes an input file based on a template with some substitutions applied. We’ll do this using a built-in TemplateWriterTask that can help create such files.
Executes a script using ScriptTask that reads the input file and produces some output. In our test case, it will just count the number of words in that file. However, this code could be any program, for example a chemistry code.
Copies all your outputs to your home directory using FileTransferTask.

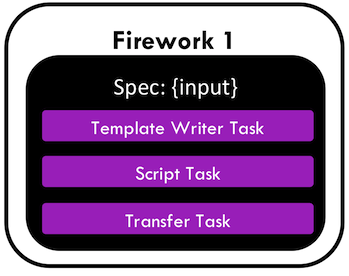
The three-step Firework thus looks like this:

Navigate to the tasks tutorial directory in your installation directory:
```
cd <INSTALL_DIR>/fw_tutorials/firetask
```
Look inside the file fw_multi.yaml:
```
spec:
  _tasks:
  - _fw_name: TemplateWriterTask
    context:
      opt1: 5.0
      opt2: fast method
    output_file: inputs.txt
    template_file: simple_template.txt
  - _fw_name: ScriptTask
    script: wc -w < inputs.txt > words.txt
    use_shell: true
  - _fw_name: FileTransferTask
    files:
    - dest: ~/words.txt
      src: words.txt
    mode: copy
```
There are now three tasks inside our spec: the TemplateWriterTask, ScriptTask, and FileTransferTask. The TemplateWriterTask will load an example template called simple_template.txt from inside the FireWorks code, replace certain portions of the template using the context, and write the result to input.txt. Next, the ScriptTask runs a word count on input.txt using the wc command and print the result to words.txt. Finally, FileTransferTask will copy the resulting output file to your home directory.

Note

If you would like to know more about how templated input writing works and define your own templated files, you should consult the TemplateWriterTask tutorial. A copy of simple_template.txt is given in the directory as simple_template_copy.txt (however, modifying the copy won’t modify the actual template).

Note

The FileTransferTask can do much more than copy a single file. For example, it can transfer your entire output directory to a remote server using SSH. For details, see the FileTransferTask docs.

Run this multi-step Firework on your FireServer:

lpad reset
lpad add fw_multi.yaml
rlaunch singleshot

You should see two files written out to the system, inputs.txt and words.txt, confirming that you successfully ran the first two steps of your job! You can also navigate to your home directory and look for words.txt to make sure the third step also got completed correctly.

This combination of writing a file, executing a command, and perhaps moving the results could be used in many situations. For example, you could use TemplateWriterTask to write a templated queue script, and then use the ScriptTask to submit it (e.g., via the qsub command). (note, however, that FireWorks provides more powerful methods to submit jobs through queues). Or, you could use the TemplateWriterTask to write an input file, the ScriptTask to execute a code that can read that input file, and finally the FileTransferTask to move the results somewhere.

Note

The only way to communicate information between Firetasks within the same Firework is by writing and reading files, such as in our example. If you want to perform more complicated information transfer, you might consider defining a workflow that connects FireWorks instead. You can pass information easily between different FireWorks in a Workflow through the FWAction object, but not between Firetasks within the same Firework (Workflow Model).

Python Example (optional)¶

Here is a complete Python example that runs multiple Firetasks within a single Firework:

from fireworks import Firework, FWorker, LaunchPad, ScriptTask, TemplateWriterTask, FileTransferTask
from fireworks.core.rocket_launcher import launch_rocket

# set up the LaunchPad and reset it
launchpad = LaunchPad()
launchpad.reset('', require_password=False)

# create the Firework consisting of multiple tasks
firetask1 = TemplateWriterTask({'context': {'opt1': 5.0, 'opt2': 'fast method'}, 'template_file': 'simple_template.txt', 'output_file': 'inputs.txt'})
firetask2 = ScriptTask.from_str('wc -w < inputs.txt > words.txt')
firetask3 = FileTransferTask({'files': [{'src': 'words.txt', 'dest': '~/words.txt'}], 'mode': 'copy'})
fw = Firework([firetask1, firetask2, firetask3])

# store workflow and launch it locally, single shot
launchpad.add_wf(fw)
launch_rocket(launchpad, FWorker())

Creating a custom Firetask¶

The TemplateWriterTask, ScriptTask, FileTransferTask are built-into FireWorks and can be used to perform useful operations. In fact, they might be all you need! In particular, because the ScriptTask can run arbitrary shell scripts, it can in theory run any type of computation and is an ‘all-encompassing’ Firetask. ScriptTask also has many additional features that are covered in the ScriptTask tutorial.

However, if you are comfortable with some basic Python, you can define your own custom Firetasks for the codes you run. A custom Firetask gives you more control over your jobs, clarifies the usage of your code, and guards against unintended behavior by restricting the commands that can be executed.

Even if you plan to only use the built-in tasks, we suggest that you still read through the next portion before continuing with the tutorial. We’ll be creating a custom Firetask that adds one or more numbers using Python’s sum() function, and later building workflows using this (and similar) Firetasks.

How FireWorks bootstraps a job¶

Before diving into an example of custom Firetask, it is worth understanding how FireWorks is bootstrapping jobs based on your specification. The basic process looks like this:

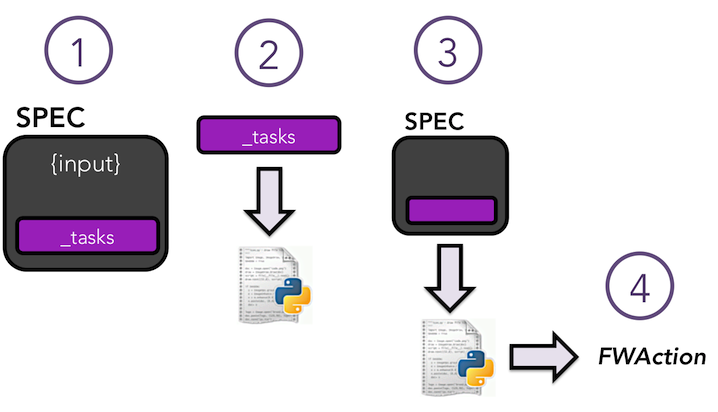
The first step of the image just shows how the spec section of the Firework is structured. There is a section that contains your Firetasks (one or many), as we saw in the previous examples. The spec also allows you to define arbitrary JSON data (labeled input in the diagram) to pass into your Firetasks as input. So far, we haven’t seen an example of this; the only information we gave in the spec in the previous examples was within the _tasks section.
In the second step, FireWorks dynamically loads Python objects based on your specified _tasks. It does this by searching a list of Python packages for Python objects that have a value of _fw_name that match your setting. When we set a _fw_name of ScriptTask in the previous examples, FireWorks was loading a Python object with a _fw_name class variable set to ScriptTask (and passing the script parameter to its constructor). The ScriptTask is just one type of Firetask that’s built into FireWorks to help you run scripts easily. You can write code for custom Firetasks anywhere in the user_packages directory of FireWorks, and it will automatically be discovered. If you want to place your Firetasks in a package outside of FireWorks, please read the FireWorks configuration tutorial. You will just need to define what Python packages to search for your custom Firetasks, or use a special format that allows for direct loading of classes.
In the third step, we execute the code of the Firetask we loaded. Specifically, we execute the run_task method which must be implemented for every Firetask. FireWorks passes in the entire spec to the run_task method; the run_task method can therefore modify its behavior based on any input data present in the spec, or by detecting previous or future tasks in the spec.
When the Firetask is done executing, it returns a FWAction object that can modify the workflow (or continue as usual) and pass information to downstream FireWorks.

Custom Firetask example: Addition Task¶

Let’s explore custom Firetasks with an example: a custom Python script for adding two numbers specified in the spec.

Staying in the firetasks tutorial directory, remove any output from the previous step:
```
rm howdy.txt FW.json words.txt
```

Let’s first look at what a custom Firetask looks like in Python. Look inside the file addition_task.py which defines the Addition Task:

class AdditionTask(FiretaskBase):

   _fw_name = "Addition Task"

   def run_task(self, fw_spec):
       input_array = fw_spec['input_array']
       m_sum = sum(input_array)

       print(f"The sum of {input_array} is: {m_sum}"

       return FWAction(stored_data={'sum': m_sum}, mod_spec=[{'_push': {'input_array': m_sum}}])

A few notes about what’s going on (things will be clearer after the next step):
- In the class definition, we are extending FiretaskBase to tell FireWorks that this is a Firetask.
- A special parameter named _fw_name is set to Addition Task. This parameter sets what this Firetask will be called by the outside world and is used to bootstrap the object, as described in the previous section. If we did not set this ourselves, the default would have been fireworks:AdditionTask (the root module name plus the class name separated by a colon).
- The run_task() method is a special method name that gets called when the task is run. It can take in a Firework specification (spec) in order to modify its behavior.
- When executing run_task(), the AdditionTask we defined first reads the input_array parameter of the Firework’s spec. It then sums all the values it finds in the input_array parameter of the Firework’s spec using Python’s sum() function. Next, the Firetask prints the inputs and the sum to the standard out. Finally, the task returns a FWAction object.
- We’ll discuss the FWAction object in greater detail in future tutorials. For now, it is sufficient to know that this is giving two instructions. The first says we should store the sum we computed in the database (inside the Firework’s stored_data section). The second will pass the results on to any downstream FireTask or FireWork in the workflow as part of the spec inside a key called input_array.
Now let’s define a Firework that runs this Firetask to add the numbers 1 and 2. Look inside the file fw_adder.yaml for this new Firework definition:
```
spec:
  _tasks:
  - _fw_name: Addition Task
    parameters: {}
  input_array:
  - 1
  - 2
```
Let’s match up this Firework with our code for our custom Firework:
- The _fw_name parameter is set to the same value as in our code for the Firetask (Addition Task). This is how FireWorks knows to run your custom Firetask rather than ScriptTask or some other Firetask.
- This spec has an input_array field defined to 1 and 2. Remember that our Python code was grabbing the values in the input_array, summing them, and printing them to standard out.
When you are comfortable that you roughly understand how a custom Firetask is set up, try running the Firework on the central server to confirm that the Addition Task works:
```
lpad reset
lpad add fw_adder.yaml
rlaunch --silencer singleshot
```
Note

The --silencer option suppresses log messages.
Confirm that the sum is not only printed to the screen, but also stored in our Firework in the stored_data section:
```
lpad get_fws -i 1 -d all
```

should contain in its output a section that looks like this:

...
"action": {
    "update_spec": {},
    "mod_spec": [],
    "stored_data": {
        "sum": 3
    },
...

Writing your own custom Firetasks¶

If you’d like to attempt writing your own Firetask, a guide to doing so can be found here.

Python example (optional)¶

Here is a complete Python example that runs a custom Firetask:

from fireworks import Firework, FWorker, LaunchPad
from fireworks.core.rocket_launcher import launch_rocket
from fw_tutorials.firetask.addition_task import AdditionTask

# set up the LaunchPad and reset it
launchpad = LaunchPad()
launchpad.reset('', require_password=False)

# create the Firework consisting of a custom "Addition" task
firework = Firework(AdditionTask(), spec={"input_array": [1, 2]})

# store workflow and launch it locally
launchpad.add_wf(firework)
launch_rocket(launchpad, FWorker())

Next up: Workflows!¶

With custom Firetasks, you can go beyond the limitations of running shell commands and execute arbitrary Python code templates. Furthermore, these templates can operate on data from the spec of the Firework. For example, the Addition Task used the input_array from the spec to decide what numbers to add. By using the same Firework with different values in the spec (try it!), one could execute a data-parallel application.

While one could construct an entire workflow by chaining together multiple Firetasks within a single Firework, this is often not ideal. For example, we might want to switch between different FireWorkers for different parts of the workflow depending on the computing requirements for each step. Or, we might have a restriction on walltime that necessitates breaking up the workflow into more atomic steps. Finally, we might want to employ complex branching logic or error-correction that would be cumbersome to employ within a single Firework. The next step in the tutorial is to explore connecting together FireWorks into a workflow.

Defining Jobs using Firetasks¶

Introduction to Firetasks¶

Running multiple Firetasks¶

Python Example (optional)¶

Creating a custom Firetask¶

How FireWorks bootstraps a job¶

Custom Firetask example: Addition Task¶

Writing your own custom Firetasks¶

Python example (optional)¶

Next up: Workflows!¶

Table of Contents

Previous topic

Next topic

This Page